IBL Algebraic Geometry: Focus on Student Presentations
Written by: Dr. Volker Ecke
This past semester, Chrissi and I co-taught an advanced mathematics major course focused on Algebraic Geometry. Our goal was to strengthen our students' preparation in reading and making sense of, presenting, and writing about mathematical ideas. We used a new (for us) format for the class, relying heavily on readings outside of class and in-class graded presentations based on Focus Questions related to those readings.
Overall Structure of the Class:
The class met once a week for 2.5h. In the week leading up to class, students worked through a significant portion of a formal mathematics textbook (Cox, Little, O'Shea: Ideals, Varieties, and Algorithms) and prepared written responses to a list of Focus Questions  with the expectation that they would be ready to present these on the board to the whole class (
with the expectation that they would be ready to present these on the board to the whole class (![]() Sample Focus Questions). Typically, we would chose a subset of "interesting" problems to be presented in class. We learned from Dana Ernst (who credits Clark Dollard) to give the students "Purple Pens" so they can revise their own drafts based on the presenters' work. This worked really well!! Finally, as part of their homework for the next class, students were asked to write up a "good version" of several of the Focus Questions along with their annotated first draft (sometimes these problems were presented, sometimes not).
Sample Focus Questions). Typically, we would chose a subset of "interesting" problems to be presented in class. We learned from Dana Ernst (who credits Clark Dollard) to give the students "Purple Pens" so they can revise their own drafts based on the presenters' work. This worked really well!! Finally, as part of their homework for the next class, students were asked to write up a "good version" of several of the Focus Questions along with their annotated first draft (sometimes these problems were presented, sometimes not).
A few observations for us:
In summary, here are a few of the observations we made in teaching Algebraic Geometry course using this approach. More details about some of these observations are included further down in this blog, or in related blogs elsewhere on our site.
- Reading formal mathematics is challenging for our students: we're now wondering how we can better support students in building this skill throughout our major program.
- Student writing improved a lot, in the sense that students included more information about their process and their thinking, so we could really get into students' heads and see more clearly what they knew, and what they were still struggling with. Read more about these "Homework Stories" in one of Chrissi's blogs.
- A Perfect Presentation has Mistakes.
- Students Revising Draft Work: Purple Pens Rock!
- We found quick, ungraded check-in surveys, or preparation rubrics, helpful in deciding what questions to have presented, who gets to present, and for which questions students may be totally unprepared, etc. Thanks to Corrin Clarkson from Columbia!
- Technology can be a valuable tool in supporting students with inquiry activities.
- Mathematics can be beautiful, and Art can motivate mathematical inquiry.
- Group work can help to digest and clarify presentations.
- One open question about this classroom structure that we're still thinking about is: how to make sure that all students get to work at their learning edge.
Technology supporting Student Inquiry:
Presentations typically involve some written work that supports the audience in making sense of the argument. For example, students can write key ideas or steps on the blackboard as they explain their ideas. Writing in real time can have the advantage of focusing everybody on the same idea, and giving the audience time to digest and reflect on the material. Some of our students also made valuable use of a document camera showing their homework write-up to guide the presentation. This way less time can be spent with writing when ideas are clear. We have also seen models where all the students selected for a presentation in a given meeting simultaneously take 5-10 min at the start of the class to write the key ideas on the board (while the rest of the class is involved in some other activity). This can be especially valuable in an intro to proof course, since students get to be deliberate before class about their choices of how much, and what, to write down.
 We opened the class with activities using the beautiful "SURFER" software from Imaginary. Surfer artists can enter a single algebraic formula, which is set equal to zero. The software then renders the geometric object corresponding to the equation (typically a surface), using pretty color schemes. The wish to create beautiful images can motivate the inquiry into the algebra: e.g. how to you create the image of a snow man; how to you show the intersection of two geometric objects.
We opened the class with activities using the beautiful "SURFER" software from Imaginary. Surfer artists can enter a single algebraic formula, which is set equal to zero. The software then renders the geometric object corresponding to the equation (typically a surface), using pretty color schemes. The wish to create beautiful images can motivate the inquiry into the algebra: e.g. how to you create the image of a snow man; how to you show the intersection of two geometric objects.
A project towards the end of the semester asked students to investigate, in the specific context of their "own" surface, a number of questions about the formal mathematical tools we had developed over the semester (e.g. the relationship between the Groebner bases of two varieties and the Groebner basis of their intersection). We have included two beautifully intriguing screenshots of student projects in this blog. In addition to SURFER, students also made extensive use of GeoGebra and WolframAlpha to explore computational aspects of algebraic geometry.
Reflections
Presentation Rubics
Our plan for the graded presentations in Algebraic Geometry was in part to give students incentive to put effort into the assigned reading and Focus Questions ahead of class. In other classes, we also have students share out their ideas and process with the whole class. Yet this typically happens at a time when they are clearly not done yet. Those "process presentations" are not graded and are meant to spread ideas, catch mistakes and make connections. Chrissi reflects on the evolution of our ideas around a grading rubric for presentations in her blog A Perfect Presentation has Mistakes.
Preparation Rubric
About half-way through the semester, Corrin Clarkson from Columbia shared an interesting teaching strategy on an IBL workshop email list. She asks students to fill out a simple, ungraded survey ahead of class rating their level of understanding for each of the problems they were asked to prepare. In addition, students can ask questions or suggest topics for class discussion. We immediately realized that this could provide us with additional information in deciding who would present what problem. Corrin was kind enough to provide us with a copy of her Google Survey Form, which made it fairly straightforward to collect this information every week before our class. Given that we had realized that interesting gaps and mistakes were actually desirable for our presentations, we slightly modified the rubric as indicated here:
Indicate the degree of your progress on each problem using the following scale:
4 - I am ready to present a solution to this problem, including interesting gaps and possible mistakes. (We don't expect perfect presentations.)
3 - I've made a solid start on this problem and am willing to share my progress.
2 - I have ideas about how to solve the problem, but I'm struggling to consolidate them.
1 - I understand what the problem is asking and could explain it in my own words
0 - I do not understand the problem or I haven't looked at the problem
Using Corrin's suggestions, we downloaded the data into a spreadsheet and then color coded the numerical data. 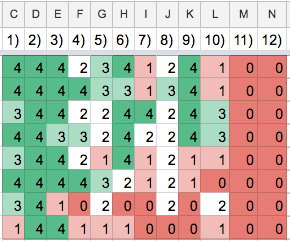 The image shows a color-coded grid for each of the 12 Focus Questions, going across from left to right. Each line corresponds to one student name (not shown here). In the picture you can see the a quick visual overview of where the class is at. We can see who is struggling or under prepared and which problems were particularly challenging. We could use this information to decide what to focus on in class and to choose who to call to the board to present what problem. This image suggests, for instance, that there is no need to present questions 2, 11, or 12--albeit for different reasons. Based on just this data which questions would you be curious about for an engaging presentation that could advance most students' learning in this class?
The image shows a color-coded grid for each of the 12 Focus Questions, going across from left to right. Each line corresponds to one student name (not shown here). In the picture you can see the a quick visual overview of where the class is at. We can see who is struggling or under prepared and which problems were particularly challenging. We could use this information to decide what to focus on in class and to choose who to call to the board to present what problem. This image suggests, for instance, that there is no need to present questions 2, 11, or 12--albeit for different reasons. Based on just this data which questions would you be curious about for an engaging presentation that could advance most students' learning in this class?
Where we initially wanted to use the Presentation Rubric to encourage students to put effort into being well-prepared for class, we are using this Preparation Rubric to communicate the importance of student effort in a better way.
Presentations and Giving Questions back to the Class
When questions arose around the presenter's work (or around the bigger mathematical picture), we typically collaborated as a class to help us all make sense of this idea. Occasionally, the presenter and the audience all needed to think more deeply about a particular important concept, idea, or technique. In such situations, we sometimes decided to stop the presentation and send the students into small groups to make sense of a particular important question. We want to highlight this choice as another important teacher tool in an inquiry classroom: Depending on the situation, we can locate responsibility for sense-making somewhere along the continuum between just the presenter, all the way to the whole class, and make choices in the classroom accordingly. Because this approach of giving questions back to the class is so natural in our other IBL classes, it was only during reflections at the end of the semester that we realized that this was a component we hadn't typically seen in other presentation-focused inquiry classes. It's wonderful to identify another "control knob" to adapt the learning environment to the goals, needs, and flow of student inquiry.
Focus Questions for Learning, for Presenting, for ...
We also noticed that some of our Focus Questions did not make for good presentations: "Explain in your own words how you make sense of this proof" often prompted deep thinking but did not make for interesting, engaging, or accessible presentations because students would just read several dense pages of their writing. At the other end of the spectrum, we realized that computation-focused exercises from the book often needed a more explicit prompt for students to reflect on, and explain the bigger point of this exercise. Reflecting more deeply we realized that the Focus Questions serve several purposes: on the one hand, to engage students in activities to deepen and challenge their thinking during the reading; on the other hand, to present some coherent of mathematics to the whole class. We are using this lens to review our Focus Questions critically in preparation for teaching this class again, hopefully in another year or two.
Work in Progress: Differentiation
One aspect of running a presentation focused class that we have not quite figured out yet is how to differentiate the class well enough so that all students are working at their learning edge. We have a good sense of how to do this is inquiry based classes where the focus is on group work and whole class discussions. In her blog "Inquiry is Differentiation" Chrissi summarizes some of the structures in a group setting that allow for wide differentiation of pace, tools, scaffolding, encouragement, extension questions, etc.
When our focus was on presentations, it seemed that the whole class is for much of the time focused simultaneously on one particular presentation by one particular presenter.  While all students are expected to have prepared the material themselves, it is our observation that there will be variation in the depth, tools, representations, and other dimensions of their preparation. Some students seemed overwhelmed or lost in some presentations (busily copying down the presenter's notes). For others the material in some presentations was so clear that they looked like they could recite the argument along with the presenter. What could we do in this presentation focused format to provide both groups with more learning opportunities at their learning edge?
While all students are expected to have prepared the material themselves, it is our observation that there will be variation in the depth, tools, representations, and other dimensions of their preparation. Some students seemed overwhelmed or lost in some presentations (busily copying down the presenter's notes). For others the material in some presentations was so clear that they looked like they could recite the argument along with the presenter. What could we do in this presentation focused format to provide both groups with more learning opportunities at their learning edge?






