Pennies & Paperclip Proofs
Written by: Dr. Julian Fleron
Pennies and Paperclips is a two-player game played on a 4 by 4 checkerboard with a standard color pattern. One player, "Penny", gets two pennies as her pieces. The other player, "Clip", gets a pile of paperclips as his pieces. Penny places her two pennies on any two different squares on the board. Once the pennies are placed, Clip attempts to cover the remainder of the board with paperclips — with each paperclip being required to cover two adjacent squares. Paperclips are not allowed to overlap. If the remainder of the board can be covered with paperclips then Clip is declared the winner. If the remainder of the board cannot be covered with paperclips then Penny is the winner.
If you've not played it before, try it. See if you can find the winning strategies. [Hey, you are here because of some interest in inquiry-based learning. You try it!]
The winning strategy for Penny is to occupy two squares of the same color. Paperclips must cover one black and one white square with each move and Penny will have broken the parity with her play.
Students readily discover both winning strategies after playing and recording eight to a dozen games. The proof that this strategy is a winning strategy for Penny generally comes not long after that — a 50 minute class period is certainly sufficient to move from the introduction of the game, through game play/data collection, and well into the reasoning to proof phase.
Having dispatched with the proof for the winning strategy for Penny, students are too eager to give the dual argument as a proof for Clip. That is, they are quick to say, pennies occupy one white and one black space. This leaves 7 black and 7 white, exactly the correct number of empty spaces — of the correct parity — for paperclips. Lost in this reasoning is that there is no guarantee that the paperclips can be arranged to utilize all of these spaces.
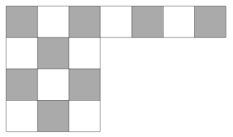
The exact same argument can be made if the gameboard is the one shown above. But paperclips cannot be appropriately placed in all situations where Penny has played one black and one white space. I.e. this illustrates the gap in reasoning in the students' parity argument for paperclips' winning strategy.
This stumps students. One approach is to introduce a Hamiltonian path which provides a path to guide the placement of the paperclips. I showed students a general Hamiltonian path on a complex network and wondered aloud if such a thing could be useful if found for their checkerboard.
Many students took the bait. Proofs 1-3 utilize this approach. ![]() Proof 1 is quite minimal, but covers all of the necessary points.
Proof 1 is quite minimal, but covers all of the necessary points. ![]() Proof 2 is slightly longer and in
Proof 2 is slightly longer and in ![]() Proof 3 you begin to see what we refer to in our paper as the narrative structure of proof. The student has a story to tell — her proof includes a context, main characters, and a story arc of what she discovered.
Proof 3 you begin to see what we refer to in our paper as the narrative structure of proof. The student has a story to tell — her proof includes a context, main characters, and a story arc of what she discovered.
As happens with inquiry, there are always alternative approaches. Several groups found nice ways to categorize the different configurations of pennies that are possible and treat each case separately. ![]() Proof 4 is a really nice example of this.
Proof 4 is a really nice example of this.
