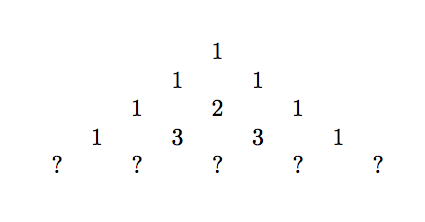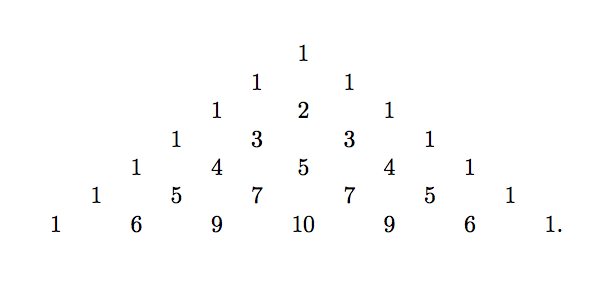Tackling Rascals’ Triangle - How Inquiry Challenges What We Know and How We Know It

Written by: Dr. Julian Fleron.

We present the following case study as a way of illustrating the power of inquiry-based learning to transform how we think about what we know and how we know. It challenges us to reconsider the nature of teaching and learning in mathematics.

Question: What is the next row in the following triangular pattern of numbers:

The archetypal answer from a mathematically trained audience - "Ah, yes. Good old Pascal’s triangle. The next row is $1 \quad 4 \quad 6 \quad 4 \quad 1$."

Let us think about this answer. Mathematically it suggests a lack of conscious awareness of the limitations of inductive reasoning or what Richard Guy called the "Strong Law of Small Numbers." (For more on the limitations of inductive reasoning see "Types of Reasoning" in DAoM – Truth, Reasoning, Certainty & Proof, "Patterns and Proof" in DAoM – Patterns and our blog on "Inductive and Deductive Reasoning.")

Ontologically this answer is really a byproduct of operant conditioning. You have seen Pascal’s triangle many times before, you recognize it and you feel compelled to provide the "correct answer."

This answer, in and of itself, demonstrates little or no mathematical understanding of value. As a superior alternative we propose:

Question: Can you find a triangular pattern of numbers which begins:

If so, what can you learn about this number pattern?

This is a story of one such pattern and the wonderful new things that three different groups, and their teachers, learned about it.

"The question is not what you look at, but what you see."
[Henry David Thoreau]

Rascals’ Triangle

In 2010 a seventh grader and two eighth graders challenged the first question, asked on an I.Q. test, deciding instead to answer the second question. What they invented, and shared in a paper in the College Mathematics Journal [``The Rascal Triangle,’’ Alif Anggoro, Eddy Liu and Angus Tulloch, The College Mathematics Journal, Vol. 41, No. 5, pp. 393 - 395] was the beautiful pattern now known as Rascals’ triangle:

What a remarkable pattern. Notice how the entries in column m increase by m, starting from 1.

Beautiful.

And much more natural than Pascal’s triangle.

How surprising that it had not been seen before. For centuries we’ve all been giving the "correct answer," unable to see with our own fresh eyes.

In their paper the Rascals describe how their teacher challenged them to find a defining rule for their triangle, much like Pascal’s formula has the formula West + East = South. What the Rascals found was the defining rule
\[ \frac{West \times East + 1}{North}=South.\]
As it involves division, their teacher upped the ante by challenging them to prove this formula always resulted in an integer. To do this the Rascals used the growth along column m to derive the expression mn+1 for entry n in column m in Rascals’ triangle. To prove their defining rule was correct, the Rascals needed to show

\begin{align}
\frac{West \times East + 1}{North} & = \frac{(m(n+1)+1)((m+1)n+1)+1}{mn+1}\\
& = (m+1)(n+1)+1\\
& = South.
\end{align}

While nontrivial, this algebra is not too complex. After reminding the reader how complex the expression for the general term in Pascal’s triangle is, the Rascals conclude their paper by asking, "Which triangle is simpler now?"

Awesome.

And profound.

What our students know is often quite different than what we "know." In the context of an inquiry-based classroom these differences can come to light – often in important ways.

Rascal Redux I

As part of an introduction to proof course for first-year mathematics majors I "introduced" Rascals’ triangle. We’d already investigated Pascal’s triangle showing that the complex expression for the binomial coefficient n choose m satisfies West + East = South and it has the same initial conditions as Pascal’s triangle so the binomial coefficients must be the correct expression for all of the entries. (And we were soon to do the same with Binet’s formula for the Fibonacci numbers.) After telling the story of Rascals’ triangle, much like above, I sent the students on their way to discover an equation for the general entry in the triangle and to prove that it satisfied the defining rule given by the Rascals. I’d consulted briefly with the paper and told the students exactly what to do – no problem.

Students poured into my office hours. Soon it was clear how algebraically intense the task I had set them on was. My quick rereading of the Rascals’ paper had glossed over the fact that they parameterized their triangle by the entries along diagonals. With my well-developed Pascal’s triangle conditioning I saw the variables n and m and immediately interpreted them as denoting the rows and columns. The Rascals had been quite explicit about these terms denoting the nth entry along column m. My conditioning blinded me.

So here’s the task I had set my students on. Using r to represent the typical, horizontal row and m to represent the column the general entry in Rascals’ triangle is
\[ m(r-m)+1.\]
While the students did successfully develop this formula, it implicitly required a change of variables away from the defining nature of Rascals’ triangle. And then the algebraic equation one needs to justify to assure the Rascal’s diamond rule is true is:
\[ \frac{\left( m(r+1)-m^2+1\right) \times \left( (m+1)r –(m+1)^2+1 \right) +1}{m(r-m)+1}=(m+1)((r+1)-(m+1))+1.\]

Ugh. What a mess I had lead students into.

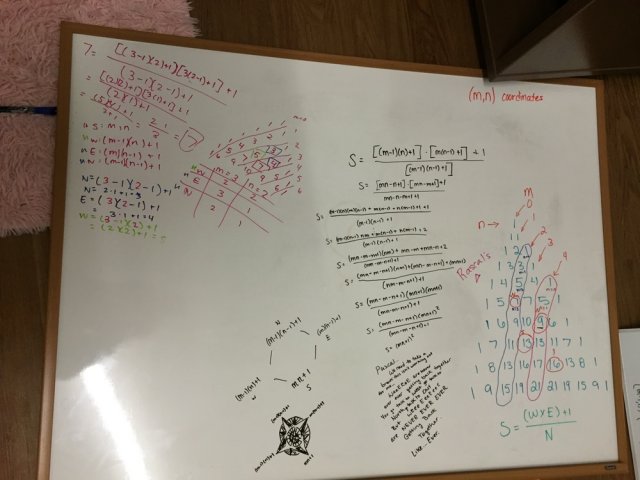
Was there any real learning going on here for all of the effort? Or was this just an intense algebraic workout which had enough opportunity to go wrong that almost all students were frustrated? Pictured below is some of the work of one group of students. Notice the beautiful compass rose for the Rascals’ diamond pattern. But notice also the Taylor Swift parody – what was meant to inspire inquiry had turned into a narrow slog.

Pascal…
We need to take a break this isn’t working out for me…
WeeEEeE are never ever ever getting back together again.
You go talk to West go talk to North go talk to East
But wEeeEeeEeeE are NEVER EVER EVER
Getting Back Together
Like… Ever

Rascal Redux II

Meanwhile, from this morass I decided to "introduce" Rascals’ triangle in a more open-ended way in my mathematics for liberal arts course where the semester topic was patterns. Throughout the semester students were to analyze patterns, to uncover where these patterns came from and prove whether they continued. We used the word "morphogenesis" to describe the process of pattern formation that we searched to understand.

We’d briefly investigated Pascal’s triangle and had also investigated linear growth patterns. We deferred considering the general term of Pascal’s triangle until later in the course. I introduced the story of Rascals’ triangle, much like above.

But then I didn’t do anything. I just got out of the students’ way.

As they poked around they quickly focused on the linear growth along columns. They quickly found the formula mn+1 for entry n in column m. I then wondered aloud whether there was a formula like Pascal’s West + East = South. Work seemed a bit slow to me. But then, I knew the answer.

One group of students asked me to check out their idea. They had formulated a rule and had some evidence in support of their rule. I saw immediately that it was much too simple to work. I told them it was an interesting rule and asked them to check some more examples. I gave no hint that there was anything wrong with it, but as I turned to go I was certain that they would quickly find a counterexample and I was no longer needed. I knew this because I knew what the rule was. "But we’ve checked all of these" they said. I returned with greater focus. With my privileged knowledge of the correct rule I had not recognized that they had checked more than a dozen examples.

I was unnerved. It couldn’t be this simple. I wondered to myself, "What am I missing?" "What do I tell them?" Several other groups had questions. As a way out I sent this group over to see if they could help another group and I moved on hoping that they and I would find some clarity. The next group I visited? They had the same simple formula! "What is going on?!" It was happening quickly and I was totally unprepared for it. I quickly left them too, shaking my head – willing now to let students see that I was quite confused. The next group had given up and looked up the Rascals’ paper. Now there were two formulas in play. This was the perfect opportunity to let students debate the merits of their approaches. I could watch and catch up.

So groups shared. Both rules went up on the boards. The easier rule was:
\[West + East + 1 = North + South.\]

Using the power of numbers we checked both rules for many examples. And both seemed to work.

Now we were all confused. How could there be two different rules?

I encouraged the class to prove the rules were correct using the formula they had built. All gravitated to the easier formula. And soon they had it:
\begin{align}
West + East + 1 & = (m(n+1)+1) + ((m+1)n+1) + 1 \\
&= mn + m + 1 + mn + n + 1 + 1\\
&= (mn+1) + (mn + m + n + 1+1)\\
&= (mn+1) + ((m+1)(n+1)+1)\\
&= North + South.
\end{align}

They were right! There is a much easier formula for Rascals’ triangle. I couldn’t see something different, but my students could.

New Mathematical Discovery!

This new mathematical discovery and its proof below are by Westfield State students Alexis Bates, Mitchell Begin, Brianna Cora, Darryl Denson, Mary Donnelly, Cameron Earle, Elizabeth Gallagher, Edward Gard, Brandon Hammer, Caitlyn Hurley, Ross Lewicki, Devorah Lipschitz, Thomas Moore, Constance Morgan-Poirier, Barbara Nguyen, Matthew O'Connor, Katherine Parent, Taylor Powers, Amanda Sheldon, Courtney Smith, Jonathan Tumblin, Cameron Vujs, Miranda Weathers, Jonathan Whalen.

Subsequently we have looked and it appears that despite the wide interest in Rascals’ triangle, nobody has seen this far easier rule! So, together we started to write up the story of our adventure with Rascals’ triangle. [To be submitted to the College Mathematics Journal. A draft can be downloaded here.]

Yet we were still bothered about the "morphogenesis" – where’d these formulas come from and why were they really true? As we thought about how the diamond formula was related to the linear growth patterns, there was a great idea! The two sides of the diamond are simply consecutive, corresponding terms along successive columns. So the first differences along one side are simply one more than those along the other. In other words,

\[West – North +1 = South – East.\]

Rearranging we have the simple rule discovered by the students.

This captures the "morphogenesis."

In the spirit of having new eyes, we thought the Rascals would appreciate the question that ends our paper: "Whose rule is simpler now?"

"Discovery consists of looking at the same thing as everybody else and seeing something different."
[A. Szent-Gyorgi]

Inquiry – What We Know and How We Know It

We started by considering what we know as it relates to extending a pattern. Notice that what we know changes several times in the story of Rascals’ triangle. And each time the matter of what we know is inextricably intertwined with how we know it.

The opportunity to inquire is what helped the Rascals and my liberal arts students to discover this wonderful triangle and to unlock its real inner-workings. This is a deep lesson.

If inquiry can give rise to such rich student discoveries stemming just from Pascal’s triangle, think of what it can do to challenge our ideas of what we know and how we know it in our mathematics classes on a day to day basis.