Mathematics, Liberal Arts, Common Visions and Guiding Symbols

Written by: Dr. Julian Fleron.

In your core/general education courses, do you make time to check in with your students about the role and value of the course in their educations?

Recently we have made a conscious effort to do this more explicitly.

We have found that having students think about the bigger picture has been motivating to them and it has helped assuage some of the negative attitudes that are often quietly carried through the course without opportunities to be addressed. "When will we ever use this?" "Why do we have to explain our work?" "Why won’t you tell us how to do it?" These questions disappear when allowed the light of the larger context of their educations.

There have also been benefits for us – it has prompted us to be more thoughtful and responsive to the big-picture matters. We encourage you to engage with your students in some of these conversations. Below we share some of the high points that have provided nourishment for these conversations.

Marketable Skills

When formally recommending students for jobs and professional or graduate schools there are typical skills where we are asked to report the ability level of the candidate. Does the candidate rank top 5%? Top 10%? Etc. When asked to name the skill areas that are included, students create fairly accurate lists. These include:

• Problem solving
• Critical thinking
• Written communication skills
• Oral communication skills
• Reading comprehension
• Ability to work well with others
• Initiative and motivation
• Leadership
• Creativity
• Academic achievement

It’s reassuring that our liberal arts students see this.

But there is an ironic dichotomy at play here. While students recognize this is what employers and professional and graduate schools are looking for, they somewhat hostile to the common core/general education programs that are designed to help them develop precisely these skills. They don’t know what the liberal arts are, they do not know what the goals of a liberal arts education are and they relatively sure that they would be much better off if they could spend all four years of college taking courses in their major.

In fact, these skill areas are central to the Common Visions report and College Learning for the New Global Century (described below), and are fundamental goals of the Mathematical Explorations course that they are enrolled in! A reminder of how they are building these skills every day in the class is enlightening, and provides a good opportunity to open a dialogue about these larger issues.

Common Visions – The New Common Vision Reports and DAoM Student Goals

Last month the Common Vision report for undergraduate mathematical sciences programs in 2025 was released. The Common Vision report is designed to integrate earlier reports on the undergraduate program in mathematics "into a single set of recommendations" and to provide "a snapshot of the current collective thinking about undergraduate education in mathematics and statistics." [p. 3] It is an important report which was developed jointly by leaders of the American Association of Two-Year Colleges, the American Mathematical Society, the American Statistical Association, the Mathematical Association of America and the Society for Industrial and Applied Mathematics.

Look at recommendations from the Common Visions report highlighted below. Are the curricula in your core/general education courses compatible with these recommendations? Are there ways you could make it embrace some of these areas more fully?

After an introduction and review of the existing recommendations, the first substantive section of the report addresses "common themes." Curricula is the first topic addressed and the report recommends [p. 12-3]:

All the guides agreed that instructors should present key ideas and concepts from a variety of perspectives, employ a broad range of examples and applications to motivate and illustrate the material, promote awareness of connections to other subjects, and introduce contemporary topics and their applications. Instructors should intentionally plan curricula to:

• Enhance students’ perceptions of the beauty, vitality, and power of the mathematical sciences.
• Enhance students’ understanding of mathematics as a creative endeavor.
• Increase students’ quantitative and logical reasoning abilities needed for informed citizenship and for the workplace.
• Increase students’ confidence and joy in doing mathematics and statistics.
• Improve students’ ability to communicate quantitative ideas orally and in writing (and since a precursor to communication is understanding, improve students’ ability to interpret information, organize material, and reflect on results).
• Encourage students to continue taking courses in the mathematical sciences.

These are valuable recommendations. As we asked ourselves how well our curricula was aligned with these recommendations we went back and looked at the Student Goals for the Discovering the Art of Mathematics project. Described first in 2009 and then revised in 2012, our goals are:

Student learning and growth is at the heart of our project. To be transformed, our students grow in many areas, discovering powerful relationships between themselves, the world, society, patterns, rigorous thinking, and communication. The specific goals for student learning are:

1. Students will appreciate mathematics as a human endeavor which is one of our most fundamental intellectual pursuits.
2. Students will understand that mathematics is a vital, rapidly growing field of inquiry with a dedicated cohort of practitioners.
3. Students will understand the continued impact of mathematics in shaping history, culture, logic, philosophy, and knowledge, as well as its role as a humanistic and aesthetic discipline.
4. Students will understand the ubiquitous role of mathematics in the world around them.
5. Students will strengthen their reasoning skills and become better problem solvers.
6. Students will strengthen their skills in reading, writing, argumentation and speaking.
7. Students will become more self-monitoring, reflective learners and take greater personal responsibility for their learning.
8. Students will approach mathematics more positively and gain a balanced perspective of mathematics.
9. Students will improve their mathematical confidence.
10. Students will develop awareness of the negative impact of broadly-held societal views.
11. Students will be capable of and interested in considering mathematics outside of the confines of the classroom, understanding the value of life-long learning in mathematics.

Wow! That’s pretty encouraging!

With renewed attention from such a significant policy document, we took another step back to look at the big picture. Who are these students that we teach?

Mathematics for Liberal Arts

In typical fall semester in the U.S. over 230,000 two- and four-year college students enroll in a mathematics for liberal arts (MLA) course. This audience is the fifth largest cohort of undergraduate mathematics students.

Repeatedly the Common Vision report tells us the status quo is unacceptable. What is this status quo in MLA? According to the 2005 CBMS report, 55% of MLA students at four-year colleges are typically taught by faculty who are neither tenured nor tenure-track. By 2010 the situation was worse, with 60% of MLA courses taught by faculty that were neither tenured, tenure-track nor permanent at 4-year bachelors granting colleges and universities; 66% of MLA courses were taught by such faculty at masters granting institutions; and 84% of MLA courses were taught by such faculty at PhD granting institutions. (In fact, 20% of MLA sections at PhD granting institutions were taught by graduate students.) [2010 CBMS report.] This is not emblematic of deep, institutional commitments to such an important audience.

Statistics regarding pedagogy, while limited, are also bleak. The 2005 CBMS report [59] reports that 79% of MLA courses at two-year colleges were taught using the “standard lecture mode.” By 2010 this rate had risen to 88%! [2010 CBMS report, p. 146]

For such an important course, these are disheartening statistics.

The Common Vision report is Phase I of a two-part initiative with Phase II being "an outward-looking period focused on widespread dissemination and large-scale implementation of modernized curricular and delivery methods." We believe that the work of Discovering the Art of Mathematics can serve as a prime example for MLA.

Through its workshops, presentations, papers and the e-book "Teaching and Learning Mathematics Using Inquiry," Discovering the Art of Mathematics is increasingly reaching out to broader audiences beyond MLA where inquiry-based learning can play important roles in pedagogical advances. Since the curriculum that makes up the eleven learning guides was developed with MLA students as a primary audience, we can zoom out farther and think about the majors of our students.

The Liberal Arts and Liberal Education

Originally, in the medieval period, the liberal arts numbered seven fields that were formed into two groups: the trivium (grammar, logic and rhetoric) and the quadrivium (arithmetic, geometry, music and astronomy).

In the contemporary setting the liberal arts includes subject areas where advanced mathematical education is essential – biology, astronomy, physics, economics and mathematics itself. But the other subject areas falling under the liberal arts umbrella have entirely different needs. These areas include: music, fine arts, performing arts, languages, literature, philosophy, psychology, religious studies, geography, political science, sociology, and history.

Think about these students. What are their needs? Their interests? In what ways will a mathematics course be of value to them, now or in the future?

Our position is that these students have generally been disfranchised from mathematics. As we have noted, MLA has been somewhat marginalized. Instead we see it as an important opportunity to empower these students. We can do this through curriculum – where they see real connections between mathematics and their interests. The connections between mathematics and art, history, dance, philosophy,… are broad and rich through the Discovering the Art of Mathematics volumes. Moreover, they can be empowered through a pedagogy which involves them and which allows them to recover from painful or deficient experiences with mathematics in their past.

What is a liberal education? Liberal Arts is derived from the Latin artes liberales. Liberales means "worthy of a free person." Artes are arts – skills and abilities to make, work with and understand things. Increasingly, liberal education is defined "not as a discrete set of disciplines… but rather as a comprehensive set of aims and outcomes that are essential both for a globally engaged democracy and for a dynamic, innovation-fueled economy." [p. 11 of the AACU report College Learning for the New Global Century.]

Like our students’ views of the common core/general education, "in the wider society, many still see liberal education as the `nonvocational’ or `less marketable’ part of the curriculum." However, "That twentieth-century view is now obsolete… In an economy fueled by innovation, the capabilities developed through a liberal education have become America’s most valuable economic asset… The aims and outcomes of a liberal education are essential to our nation’s future." [pp. 13-4 of College Learning for the New Global Century.]

And what are the "essential learning outcomes" in a liberal education? From College Learning for the New Global Century, they are:

• Knowledge of Human Cultures and the Physical and Natural World

• Through study in the sciences and mathematics, social sciences, humanities, histories, languages, and the arts
• Focused by engagement with big questions, both contemporary and enduring.

• Intellectual and Practical Skills, including

• Inquiry and analysis
• Critical and creative thinking
• Written and oral communication
• Quantitative literacy
• Information literacy
• Teamwork and problem solving
• Practiced extensively, across the curriculum, in the context of progressively more challenging problems, projects, and standards for performance

• Personal and Social Responsibility, including

• Civic knowledge and engagement—local and global
• Intercultural knowledge and competence
• Ethical reasoning and action
• Foundations and skills for lifelong learning
• Anchored through active involvement with diverse communities and real-world challenges

• Integrative Learning, including

• Synthesis and advanced accomplishment across general and specialized studies
• Demonstrated through the application of knowledge, skills, and responsibilities to new settings and complex problems

What points of contact do these learning outcomes have with those in your courses? With those in the Common Vision report? Can you see how Discovering the Art of Mathematics can help meet these outcomes?

Discovering the Art of Mathematics’ yantra

Designed and illustrated by Julian Fleron, George Ramirez, and Elaine Devine the symbol/yantra/mandala/logo for the Discovering the Art of Mathematics project is:

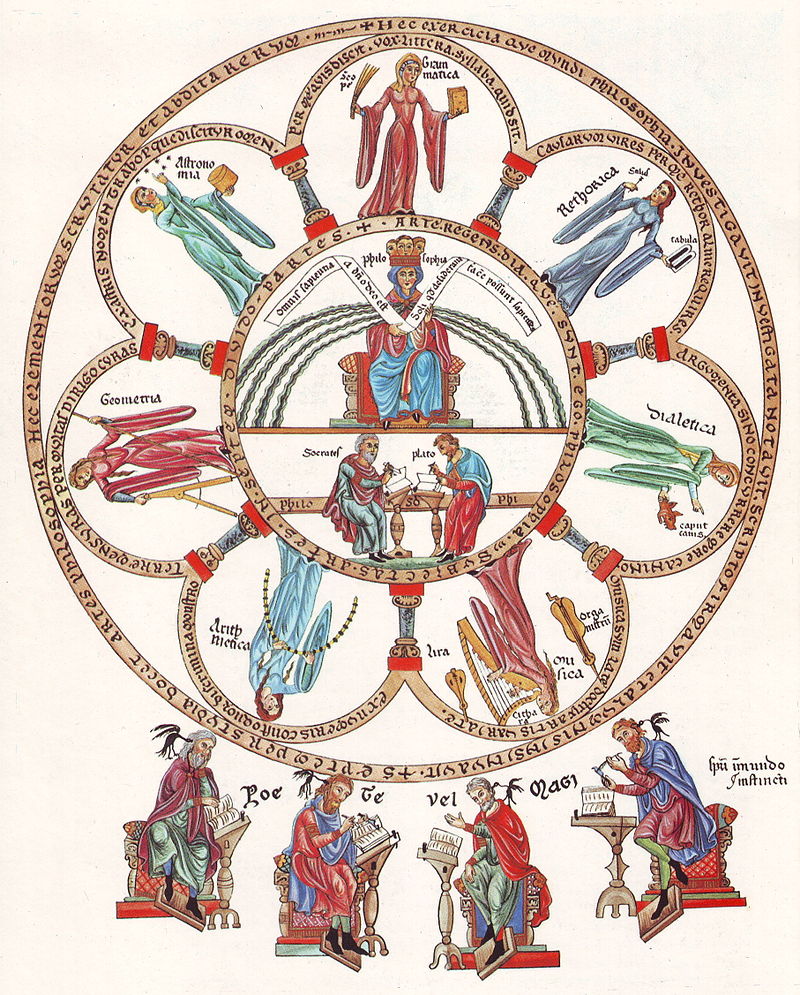
This logo is adapted from two well-known sources. The first is da Vinci’s "Vitruvian Man" which stands in the center of the logo. It is no accident we have chosen something from da Vinci – he represents the ideal of the liberal arts tradition, someone who contributes through the fine arts, music, history, literature, writing, astronomy and mathematics. The second inspiration for our logo is the "The Seven Liberal Arts" by Herrad von Landsberg. The image is from her book Garden of Delights, an important illustrated encyclopedia from the 12th century.

The seven figures positioned compass rose fashion about the center of von Landsberg’s mandala represent the seven classical liberal arts. We have replaced these seven figures with eleven icons – one for each of the curriculum guides in our series (number theory, calculus, patterns, infinities, games & puzzles, dance, art & sculpture, geometry, music, proof, and knot theory). The pillars in von Landsberg’s mandala are replaced by books holding up the arches.

And what of the central figures? In von Landsberg’s mandala Lady Philosophy sits in the center, symbolizing the highest learning. Beneath her Socrates and Plato are studying. In our yantra these three symbols have been replaced by a single human, in motion. This represents our students. Not only are they active, in motion, but they are at the center – symbolizing the students’ central role in inquiry-based learning classrooms.

In each of our classes we see our liberal arts students reach out to areas of mathematics that are brand new to them. These are areas that are connected to their interests. We are grateful to see the transformation as they reintegrate mathematics as an important part of their liberal educations.

Seems like a rather fitting yantra for this project, doesn’t it?