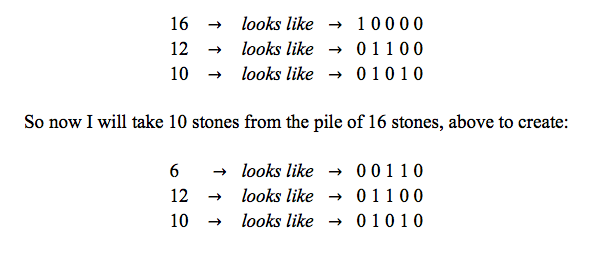The Risk of not Knowing

Written by: Dr. Christine von Renesse.

"It is definitely interesting, and definitely refreshing. It is so cool to know that the teacher isn’t holding the answer just out of reach."
[DAoM Student, Fall 2015]

"You not knowing the answer to the larger hex games made me feel a little more confident I think. More confident and I guess comfortable. It sort of put you on our level and made us all equals in the process and I knew that anything we thought of was like adding a puzzle piece to your already started plan."
[DAoM Student, Fall 2015]

I believe that students need to take risks in the mathematics classroom: the risk to not know (yet), to make mistakes, to speak up when something doesn't make sense, to ask for support, etc. In my experience this creates the environment that allows students to learn. (More in "Promoting Risk Taking in Mathematics Classrooms: The importance of Creating a Safe Learning Environment," by Prof. Sharma -- published in The Mathematics Enthusiast; http://scholarworks.umt.edu/tme/vol12/iss1/24). But this is not what this blog is about. I want to take it a step further.

If we ask our students to take risks, shouldn’t we, the teachers and facilitators, do the same? I find it easier for my students to be vulnerable when I have modeled what that could look like. Let's assume a student asks me something that I don't know the answer to. If they hear me say: "That's a great question. I don't know the answer right now, but you got me curious. What can we do to find out?" they are more likely to change their mindset towards more risk taking. With this one question I model not knowing, curiosity, persistence and team work. Other good modeling comments might be:

"Wow, that's really interesting... I need to think about this for a moment" while going to a table to work by myself.
"Let's ask the whole class about this, maybe we can find out together"?
"Tell me more, I am trying to make sense of this".
"I wonder how this connects to what we have done before"?
What do you think I am modeling with each of these comments?

As a community of mathematicians we can now start the process of exploring mathematics together. The fact that I, the professor, don't know also empowers students to find an explanation before me. The students are the true researchers and they suddenly have the responsibility to find a solution or explanation for the rest of the class. Now they want to know.

Let me describe two moments from my Math Explorations class last Fall (2015) when I took the risk of not knowing.

Nim Game

In our version of the game nim (called the "piles game" in our DAoM games book ) the two players share 3 piles of stones. At each turn the player can choose one pile and take as many stones as desired. The person to take the last stone(s) wins. After a week of hard work, and playing (and losing) against me a lot, the students discovered a winning strategy that uses binary numbers to match up subpiles of stones. At this point I usually change topics and move on. Why? Once students make sense of binary numbers and how to adjust the sub-piles they seem pretty overwhelmed…. but is this the true reason that I move on? I remember that I read a proof of the winning strategy a few years back – and that I thought it would be too “abstract” for my students. And so I didn’t bother and didn’t remember much either.

This semester I decided (in the moment) to ask the question that we have asked all semester long: why does it work? It just seemed wrong to let the reasoning go since we had proven all of our other conjectures this semester. I took the risk to not know the answer myself. I decided that I wanted us to make sense of the binary numbers and their strange connection to the piles game ourselves – or at least try and give up together.

It was interesting to see how the dynamic changed for me when I didn’t know the answer and couldn’t predict strategies. It forced me to really listen to my students’ thinking without assuming anything. And listening well is hard! I videotaped my classes 2 years ago and learned a lot from watching the videos. I noticed, for instance, that I would listen to my students for a bit, decide what they were probably trying to say, and then support them in the direction I had decided they were pursuing. Not good.

As a result of my not-knowing we had a wonderful week of classes in which even my least confident students were working on the board: finding patterns, making more conjectures, trying out arguments and being confident and persistent. And it was so cool to find out that the proof doesn't need to be "too abstract" at all. We didn't define the nim sum but instead my students worked with odd and even numbers in the sum of binary numbers. They found the complete proof themselves, working through all possible cases. My contribution came in honest questions about their thought process and looking for counter examples when I thought there were "holes" in their arguments.

And since I still wasn’t entirely sure which argument would get us to a full proof, I was very engaged in making sense of my students’ thinking. I had even more fun that usually and I got to think very hard! Was it scary? Yes, at first I was a bit worried but then in the midst of grappling with the mathematics I just enjoyed that real mathematics was happening and that everyone was engaged and stretching and learning (including me).

And how could I not take this risk (at least once in a while) when I ask my students to take this risk every single class? They never know what’s coming and need to be open to making mistakes, defending their arguments, asking questions and to keep on working. That’s a pretty vulnerable place to be in.

"From the very first moment we started the Stone Game, I was able to understand it and was actually excited to discover more ways in which a player could win. After the class ended, I remember I went back to my dorm room, tore up a piece of paper into little squares, and began to search for more ways that a player could win. After I was finished working through some of my ideas, I looked around at all the little scrapes of paper that were covering my desk, and I was amazed with myself. That had been the first time I had ever gotten so excited about working on a math problem outside of the classroom."
[DAoM Student, Fall 2015]

Hex Game

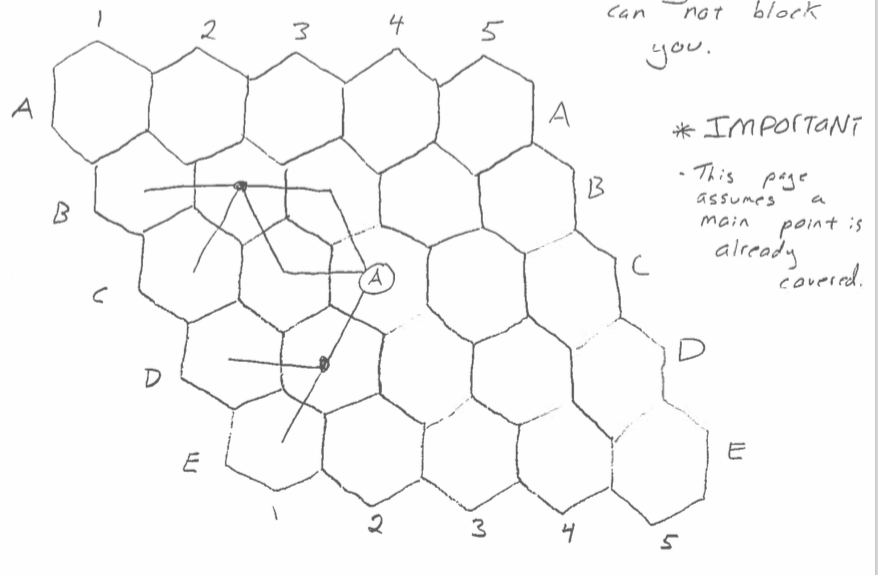
Last fall I taught the hex game in which each player tries to connect their sides of a board compiled of hexagons. We completed the proof of the winning strategy for the 5x5 board as I had done in prior semesters (see student work below). While I had played on larger boards before I had never seen a complete winning strategy for any larger board than 5x5. So I took the risk to try it out during class. Looking at the 6x6 board we immediately noticed how much more difficult it gets. There are so many more options! I wasn't sure of the winning strategy myself yet but I kept winning most games against my students probably because I am used to thinking a few steps further ahead ☺. And we did find a winning strategy for the 6x6 eventually, even though our proof/representation wasn't very elegant yet. You can see some student work of the 5x5 and 6x6 strategies below.

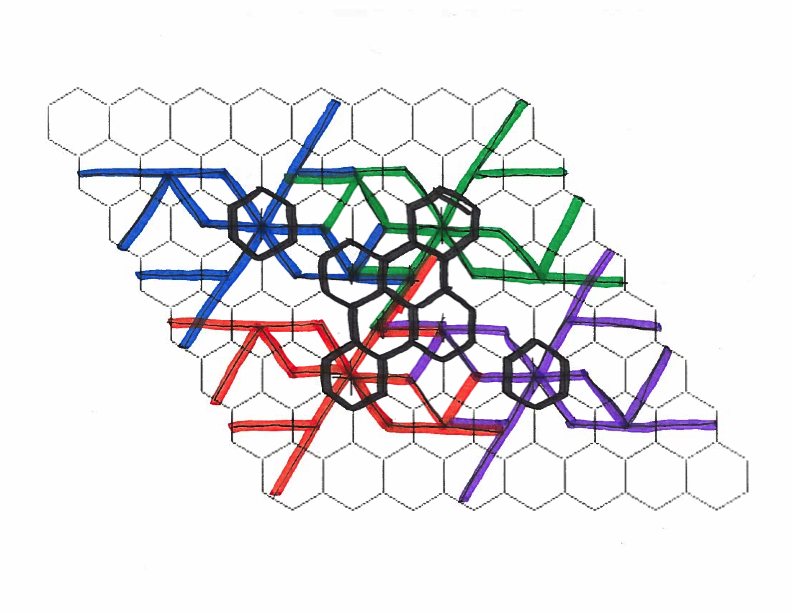
For the last day of classes I printed the 8x8 and the 11x11 board to see how our strategies translated and to show my students what the "actual" game looked like. I did find some resources that seem to explain existing winning strategies for larger boards but I found myself resistant to read them and decided to hold off until class so I didn't spoil the fun. The students were super excited to work on the 8x8 board and kept trying out their strategies against me. And after classes were done some students came to show me what they were working on to prove their winning strategy, see image below. They were using their solutions of the 5x5 board to create paths in the 8x8 board - what a great idea. While I didn't think that they had the complete answer (yet) I was so happy to see them work self motivated on a hard problem after classes were done.

"I believe that it was exciting that you did not have an answer because it gave J. and me the opportunity to show you something new and exciting, like what you have done for us through the semester."
[DAoM Student, Fall 2015]