Steven Strogatz' Reflection (Part 1)
Teaching through inquiry: A beginner’s reflections
by Steven Strogatz.
Last fall, for the first time in my career, I tried a new way of teaching. Instead of lecturing, I gave my students puzzles and questions to explore together in small groups. What happened over the rest of that semester turned out to be the most astonishing, uplifting experience I’ve ever had as a teacher.
But before I get to that, I want to offer my heartfelt thanks to Drs. Julian Fleron, Phil Hotchkiss, Volker Ecke, and Christine von Renesse, the master teachers, coaches, and visionaries behind the "Discovering the Art of Mathematics" series. They invited me to write a blog post about what it was like to be a beginner at teaching through inquiry, and to reflect on what my students and I learned from our adventures.
Love at first sight
For the past few years I've been growing dissatisfied with the results of my usual way of teaching, which is lecturing. Although quite a few of my students seemed to enjoy my lectures, many of them weren’t engaging with the material deeply. Just watching a performance, a lecture, and then doing homework, wasn't enough to get them to learn the subject properly, to master it.
So I’d been toying with the idea of trying some more active form of teaching and learning, but I wasn't sure how to start. One day in January 2013 when I was at the big annual math meeting – the “Joint Mathematics Meetings” where the major mathematical societies come together – I was wandering around in the exhibition hall and came across an exhibit that caught my eye. There were four young professors from Westfield State who were encouraging people to play math games. They were handing out Rubik's cubes, getting people to play a game called hex, or tying knots, or even dancing and making knots with their own bodies in groups. When I took a closer look I noticed that they had workbooks strewn over their table. These were workbooks that they themselves had written for a "math for liberal arts" course that they'd been teaching for the past few years at Westfield State. These workbooks were so attractive, and so filled with interesting activities for students to do, that I started to think this could be a way for me to try teaching in a style where my students would be more active.
When I talked with these faculty from Westfield State, I was struck by their passion for what they called inquiry-based learning. I found myself coming back to their exhibit, over and over again, over the next few days. I kept bringing other colleagues to their booth to show them what was going on, to show them how cool and exciting it was. Something about it grabbed me.
And I guess what really clinched it was when Julian Fleron, one of the faculty from Westfield State, told me that they had a grant from the National Science Foundation to spread their ideas widely through the math community, and that they would be delighted to come to Cornell to give us a workshop, to show us how to make this style of teaching a reality in our courses. That was an offer I couldn't refuse. So when the time came to choose courses for 2014, I asked to teach a course that was already on the books at Cornell called "Mathematical Explorations." It turns out that a course in this active style of learning, this inquiry-based learning, already existed at Cornell and had been taught for a number of years. But I had only recently joined the math department, having spent the first 20 years of my career at Cornell in engineering. So the course was new to me. I asked to teach it.
In mid-August 2014, the Westfield State folks came to visit us and give us that workshop. They showed us how to teach in this style, and how to assess our students’ performance, and also how to approach some of the psychological issues that come up with this population of students, issues like math anxiety and math phobia. They also showed us what it would feel like to be a student in such a class. My Cornell colleagues and I were the students, working on puzzles together; the Westfield State folks were our teachers. That was important since none of us had ever been students in an inquiry-based learning classroom. We needed to know what it felt like, to have the right kind of empathy for our students.
The workshop: An immersion into inquiry-based learning
On the appointed day, about thirty of my colleagues showed up for the workshop. Several colleagues from Ithaca College also joined in. We held the event in a classroom recently reconfigured for active learning. It had six or seven small round tables, each with room for about six people to sit around it, and there were blackboards and whiteboards on all the walls, so that each table could have access to its own board.
After some good-natured chitchat, introductions, breakfast, and early-morning coffee, we sat ourselves down at the tables. The team of Chrissi, Volker, and Phil (Julian wasn't able to attend, unfortunately) then passed out our first activity to investigate. They gave each of us scissors and a piece of paper with an equilateral triangle drawn on it. Our instructions were to cut out the triangle, using only a single straight cut. In other words, we weren't allowed to simply cut around the triangle in the obvious way; only a single cut along a straight line was allowed.
Someone at my table had the idea that maybe we should fold the paper first, so that all the sides of the triangle lined up on top of each other, an idea that seemed obvious once it was mentioned. So we all held up our papers to the lights overhead, and began folding until all three sides aligned. In a matter of seconds, we had all successfully managed to solve the equilateral triangle.
Without comment, Chrissi and Volker (who were leading this activity while Phil watched) then handed a new sheet of paper to anyone who was ready for the next challenge. This new piece of paper had a rectangle on it. Same deal: hold the paper up to the light, make a few folds, line up the edges, snip, snip, success. At this point I was feeling pretty satisfied, and so was everyone else. There were smiles all around the room.
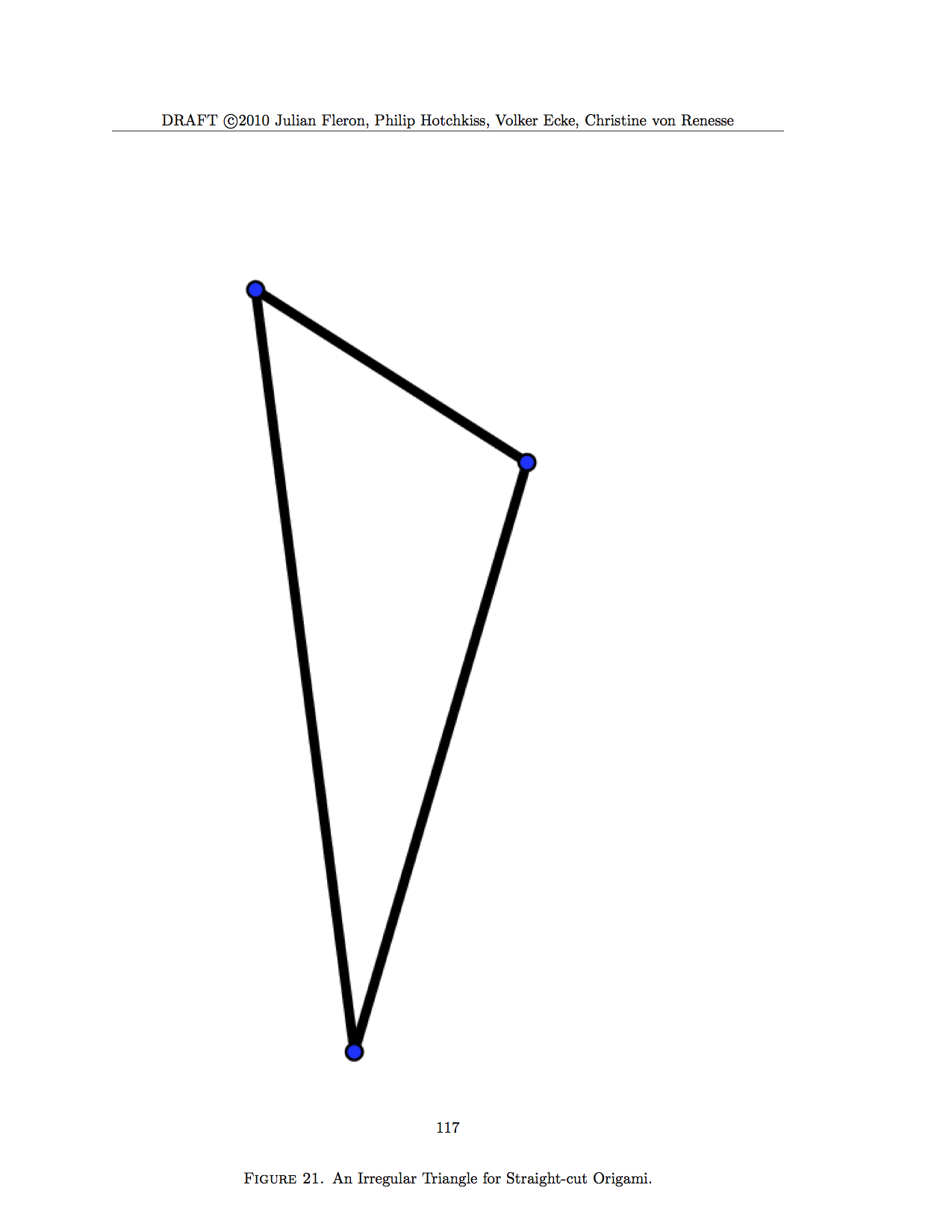
Next came a piece of paper with a scalene triangle drawn on it. This triangle was irregular and asymmetric: three sides of different lengths and none of the suggestive lines of symmetry that had been so helpful in the first two problems. The earlier tricks that worked for the rectangle and equilateral triangle weren't good enough anymore. We needed a new idea.
Someone at my table – I think it was Mike Stillman – said that maybe it was impossible to cut out a scalene triangle with a single straight cut. Maybe we were supposed to prove that it was an impossible task unless the shape had a line of symmetry. A few of us followed this line of thought for a while. Meanwhile, John Guckenheimer , sitting on my right, kept playing with his paper, holding it up to the light and looking at it from various angles, folding it gently this way and that, until he finally got it to work.
It was at this point that I began to feel uncomfortable. Even after John explained how he had done it, and everybody else at the table said “Aha!”, I still couldn't quite understand what moves he'd made. I seemed to be falling behind.
Things got worse when Volker handed John the next challenge – an irregular convex quadrilateral. John made pretty quick progress on that one too, whereas I was still mired in confusion about the scalene triangle. I could feel my face getting red. I've always been slow, but in the usual classroom setting it wasn't nearly as evident as it was now.
The rest of the room was buzzing with the happy sound of people solving puzzles together. Other tables were advancing at different rates, just as ours was, and eventually some tables went on to even harder problems, like non-convex quadrilaterals.
Mercifully, it was around this time that we paused to have a whole class discussion. Volker asked for volunteers to share what they had learned or what they had noticed, and to describe what strategies they’d used. People pointed out the importance of folding along angle bisectors, and along the perpendicular segments dropped to the sides from the point where the bisectors crossed. Volker wrote down the comments on the blackboard as people spoke, faithfully summarizing them without evaluating them.
Then, after a natural pause in the discussion, Chrissi asked, “What felt challenging about this activity?” Something about the vibe in the room – or maybe it was the way that Chrissi and Volker conducted themselves, so nonjudgmental and supportive – made me feel emboldened enough to mention how embarrassed I'd been about being the slowest at my table and not even seeing how to solve the scalene triangle. Chrissi nodded and asked me to say more. Meanwhile, nobody laughed or teased me. The classroom felt safe. Somehow, despite my anxiety about admitting my slowness in front of my colleagues, I was being made to feel valuable, as if I were contributing in a different way.
This experience gave me powerful insight into what it must be like for students in an IBL classroom. It made me realize the importance of providing a safe and nurturing space for the math explorers I was about to start working with in just a few days.
In the next part of his reflections ---- Steven shares what happened when he actually put these materials and pedagogical techniques to the test with his own liberal arts students at Cornell.