Rubik's Cube Investigations
Written by: Dr. Christine von Renesse
Why the Rubik's cube?
Solving the Rubik’s cube was one of the main themes in my Mathematical Explorations class this semester. It took about one hour of every week for the whole semester for almost all students to finish the cube, so this was a big time commitment. During the semester I regularly worried: would they all be able to solve the cube eventually? How much help do they need right now so they don’t give up? Is it worth spending so much time on a project that my students might consider a “useless skill”? It took a lot of persistence to stick with it, but we did it!
My students believed for most of the semester that they would never ever be able to solve the cube. Watching them overcome this belief was powerful. How often do you get an email in the middle of the night from non-major students in a core class just to tell you that they just solved a mathematical problem? One of the main goals of this course is for students to change their beliefs about their mathematical abilities and to become more persistent, confident and creative in problem solving. And the Rubik's cube does just that. Here is a quote from a student's journal half into the semester:
"The explorations I enjoy most are the ones with the Rubik’s cube. I never would have believed I could solve any part of the cube. At the start of the class I would’ve been happy to get one row filled with the same color. Now, I am getting closer and closer to solving the cube. It is really enjoyable to me, and I am really proud of myself with each week and with the more progress I see".
DAoM Student, Spring 2016
How is this mathematics?
At first students are very surprised to find Rubik’s cubes in a mathematics class, since their perception of mathematics is very narrow. After reading Lockhart’s lament, watching the movie “the proof”, and doing other mathematical activities and proofs (mostly from the music book) they understand that solving the cube is doing mathematics. They also connect that, just as Andrew Wiles made mistakes, they are making mistakes and need to be persistent when trying new strategies or trying to make sense of mathematics.
"This class is definitely changing my views on math. Only 2 weeks in this is easily the most rewarding and enjoyable math class I have ever taken. Between the magic trick and the Rubik’s cube and the clap and count exercise I have been thinking critically about math from day one. [...] I think the way this math explorations class is being taught is exactly how Paul Lockhart would want it to be. There’s no memorizing equations or tests, just a teacher guiding student’s through mathematical thinking. I definitely view math as one of the arts now after the argument made in this paper and hopefully math education does get reformed in the public school systems".
DAoM Student, Spring 2016"I may never need to solve a Rubik’s cube, or know the Pythagorean Theorem; but I will know how to come up with strategies to solve a real life problem or something similar. Math teaches people dedication and creativity; to never give up looking for new answers."
DAoM Student, Spring 2016
Algebra and reasoning skills
But my students also acquire algebraic thinking skills. Traditionally, students in my Mathematics for liberal arts courses do not enjoy algebra. They are either able to perform the procedures but find them boring or they never succeeded in Algebra and hate it. As an example, most of my students did not know how to “foil” the expression $(x+y)^2$. At the end of the cube project the students make sense of long chains of variables that represent moves on the cube, they invert them, modify them and invent their own. My students will most likely not need the traditional Algebra skills in their lives, but being able to create and make sense of an algebraic system, if they need one, is a handy skill to have.
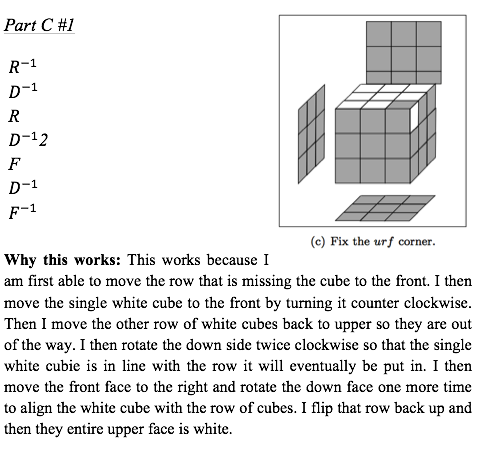
You can see in the student work to the right how a student grapples with the algebraic notation and makes sense of combining moves. The students were supposed to find a combination of moves that gets the missing white face into the top layer (there are several!), find the Singmaster notation, and explain why their moves make sense. This was an assignment during the first weeks of the semester. The student invents meaningful non-traditional notation, using $D^{-1} 2$ to express doing the move $D^{-1}$ twice, and using $MV$ to denote the middle, vertical slice of the cube.
Is solving the Rubik’s cube a procedural or a conceptual activity?
It certainly has both aspects and I want to make sure that my students learn to think conceptually about mathematics rather than procedurally. What is the point to memorize yet another procedure that allows one to solve the cube? So let’s look at where the conceptual thinking comes in:
My students have to figure out themselves how to solve the first layer of the cube. This is a very difficult conceptual activity for them. They need to make sense of:
- The difference between edge cubies and corner cubies. Students often believe that a square of some color could move anywhere on the cube and it is a big step for them to realize that for instance corner cubies can only move to other corners.
- The difference between orientation and position. A cubie can be in the correct position but in the wrong orientation.
- How to get cubies to the correct place without messing up cubies that are already in the right place in the top layer.
- How to record a chain of moves on paper and how to record the reasoning of why particular moves make sense.
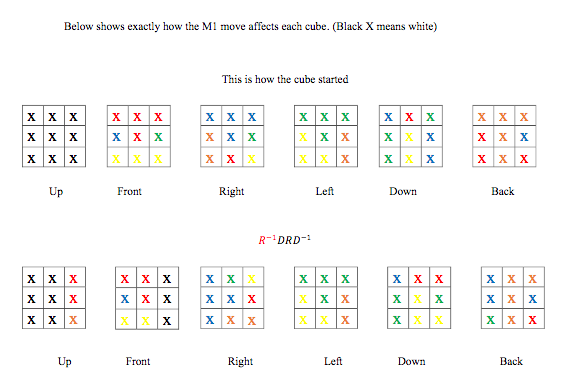
You can see in the student work to your left how students represent the changes of the cube without tracking that several faces belong to the same cubie. It took many weeks before they realized that it would be much easier to track cubies instead of cubie-faces. Interestingly I had tried to tell them that this is not the most efficient way to represent changes (and I was much less subtle than usually!) but none of them followed my lead. I think they needed to go through their own representations to make sense of what works best for them. If they still hold on to the belief that all cubie-faces can move separately then of course it doesn't make sense to track them in "groups of cubies"!
Solving the cube
There are several different strategies for solving the rest of the cube. The most common strategy, the layer method is pretty procedural and can be learned from youtube or from the instructions that come with the cube. The method we ask our students to use is the “corners first” method (See David Joyner's book). While there are also specific moves that the students receive from us, they need to investigate what exactly these moves do and how to use them. Every time they solve the cube the exact implementation will have to be slightly different which leads to a lot of thinking. There are different strategies students develop to help them figure out the rest of the cube and so there is a lot of conceptual understanding and reasoning necessary as well. But learning the Singmaster notation and correctly using the provided moves also requires students to learn and memorize some procedures.
How do I convince my students that it is a good idea to learn the "harder" method to solve the cube? I keep telling them that the goal is to reason and think hard (brain yoga!) and that there is no point in performing the easy way if we want to learn thinking a.k.a. mathematics. Some students tried both methods but no one pushed back and refused to learn the “corners first” way. And they were even prouder in the end!
An app to solve the cube...
My students found severals apps that give you explicit instructions about how to solve your specific cube, e.g. "Solve your cube" by Felipe B. Valio. At first I wasn't sure how to deal with this. Should I not permit it? (Good luck!) Should I ignore that it exists? Should I incorporate it somehow? I then realized that the app can be very helpful in analyzing the specific moves we were studying. If you have a solved cube you can see much more clearly which cubies have moved where. I asked some students if they would feel less motivated to solve the cube themselves if they had an app that could do it for them, but they didn't think so. And it turns out that they worked just as diligently on solving the cube themselves as before! The only downside was that when I scanned the room and saw a solved cube it didn't necessarily mean that it was time to celebrate.
Group work and a word of caution
Solving the Rubik’s cube seems to be a solitary exercise and it takes the students a while before they reach out to their group members for help. It is difficult for them to have conversations about the cube when they are all “stuck” at different places. Also, students have not developed a language yet to communicate with their peers about the cube. Usually it takes about two weeks for students in my classes to be comfortable with group work and the room tends to buzz with mathematical discussions. The Rubik’s cube leads to more solitary work and so it took almost half the semester before I noticed that same teamwork feeling in the room. I have to think about how I can help my students develop a sense of community earlier while working on the cube.
The Rubik's cube is a big commitment and you can't just decide to stop and switch gears like you can with some other topics. I imagine the students would be very frustrated if the topic suddenly changed or if most of them ended up not being successful in solving the cube. I believe that to be a successful facilitator of the Rubik's cube activity it is really helpful to feel comfortable in teaching inquiry-based and to have taught a mathematics for liberal arts class before. I don't think it is a great activity for "your first teaching IBL experience."
Assessment
I assess my students every class by walking around the room, listening to their conversation, asking them questions to learn abut their thinking, and watching them do mathematics. This participation grade counts for 40% of the total grade.
Almost every week my students have to complete a writing assignment about the cube. For the first few weeks, for instance, they were working on “getting the white face in the correct spot”, see student work above.
After about five weeks I checked during class (like a quiz) that every student was confident in completing the top layer. The time it took them to do this was not important to me at this point.
At the end of the semester, each student had to meet with me one-on-one and show me how he or she solved the cube. They were allowed to bring a sheet with the moves and I asked them to stop every now and then to tell me what they are planning to do next. I gave them a timeframe of 10-15 minutes to solve the cube. The time requirement had the advantage that students tried to solve the cube many times before meeting with me and had seen and solved many of the difficult situations one can face. For example: when you position the edge cubies before the corner cubies, then it can happen that you don’t have a move to deal with the last two cubies. And when you then need to use the corner swap, more of your edges are messed up again!
Open questions (for us)
There were several questions that came up for us as a class that we did not have time to make sense of:
- How do we know that the “corners first” moves will always be enough to solve the cube?
- Can we only use corner rotation and never corner swap?
- Can we only use corner swap and never corner rotation?
- Why does solving the “corners first” method lead to the fact that the edge rotation move is enough to get all edges in the right spot? Why could there not be two edge cubies left (instead of three)?
It would be great to have the time to dive into some of these questions, but a regular semester is not enough in my experience. It felt important though to acknowledge that there are open questions that we are curious about.
Extension questions
There is always at least one student who either knows how to solve the cube already or is ready to solve it in just a few weeks. This semester I had a student who first wanted to learn the layer methods and then explored the “corners first” strategies. In the end he combined both ideas and managed to solve the cube in under 1.5 minutes. He performed in front of the whole class and is planning to show off his speed cubing at a talent show at his work place.
I also brought to class the 2x2x2, 4x4x4 and 5x5x5 cubes so students who were done with the 3x3x3 cube could explore other challenges. I personally do not know how to solve the other cubes and I told my students often that I was hoping that one of them would develop a method and show me. Why? Because they need to see that we all have limits in our knowledge and that I love to learn more. I model how to be curious and admit not knowing. In doing this, students and professors are all equal learners who are curious about the world of mathematics together.
Here is a student quote from the final journal assignment:
"I can honestly say that I went from a mathematician who was worried that he wouldn’t be able to figure out the math problems given to him this semester, to a mathematician who was excited to find a new problem on the board to figure out every day and is saddened to know that this class has come to an end. However I am encouraged, because I know that from now on math will no longer worry me, and I can now say that I am pretty good at math, and feel confident in mathematics. I will continue to search for math problems to overcome, and now I have the skills to solve a Rubik's cube as well, which is something my whole life that I have always wanted to do!"
DAoM Student, Spring 2016
References:
Joyner, David. Adventures in Group Theory: Rubik's Cube, Merlin's Machine, and Other Mathematical Toys. Baltimore: Johns Hopkins University Press, 2002.